Wolfram Research es el líder mundial en el desarrollo de algoritmos
Base de algoritmos Wolfram
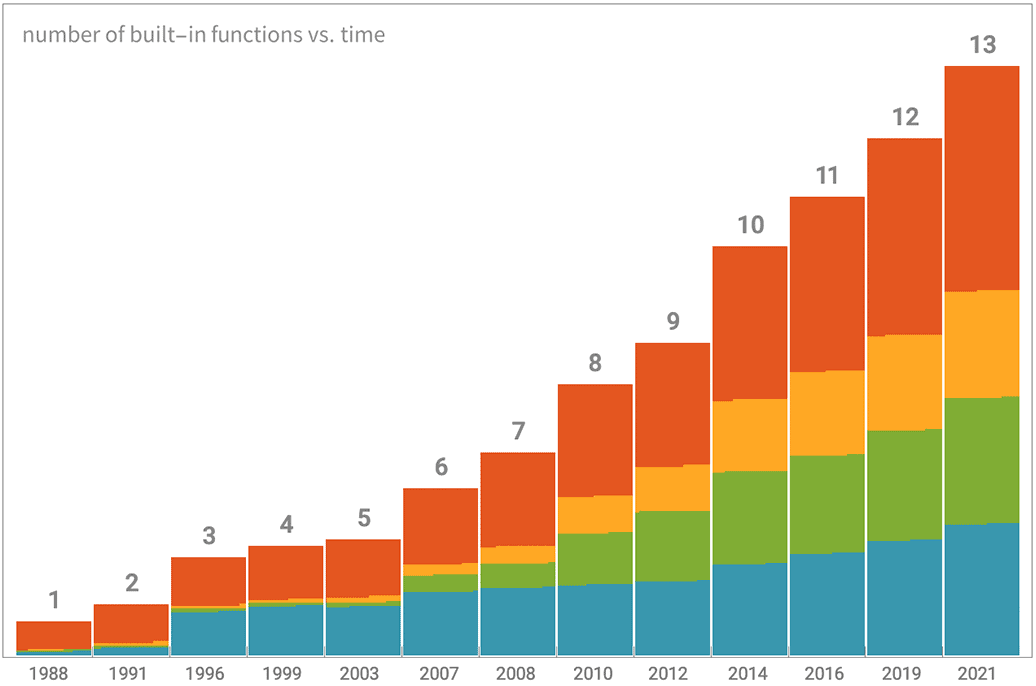
Estamos construyendo la red de algoritmos conectados más grande del mundo
Wolfram Research ha sido líder mundial en el desarrollo de algoritmos durante tres décadas, con el objetivo a largo plazo de crear una red completa de algoritmos conectados que abarque todos los tipos de computación.
De haber algoritmos conocidos, buscamos una implementación óptima; de no haberlos, buscamos inventarlos.
Decenas de miles de algoritmos es tan solo el principio. La faceta más visible de Wolfram Algorithmbase no son los algoritmos, sino los meta algoritmos, los cuales seleccionan automáticamente algoritmos específicos óptimos para usarse en cada situación distinta, permitiendo a los usuarios simplemente definir sus objetivos en Wolfram Language, y dejar que el sistema se encargue de solucionar de manera automática la mejor manera de lograrlos.
Áreas de cobertura destacadas
Computación de precisión arbitraria
Computación algebraica
Resolución de ecuaciones
Integrales simbólicas
Ecuaciones diferenciales
Álgebra lineal
Elementos finitos
Programación lineal
Programación no lineal
Optimización combinatoria
Funciones matemáticas
Manipulación de cadenas de caracteres
Estructuras de datos
Análisis de secuencias
Bases de datos
Visualización de grafos
Teoría de grafos
Geometría computacional
Reconstrucción de s
Superfunciones y meta algoritmos
La mayoría de los algoritmos específicos en Wolfram Algorithmbase son accesibles mediante superfunciones y meta algoritmos, los cuales determinan de forma automática el algoritmo óptimo para realizar una tarea en particular.
¡TAN SOLO RESUÉLVALO!
Una super función de Wolfram Language Solve se configura para resolver un rango muy amplio de ecuaciones, usando meta algoritmos para seleccionar las mejores técnicas de solución para una ecuación específica.
TANTAS OPCIONES, REALIZADAS AUTOMÁTICAMENTE
No es nada raro que una superfunción de Wolfram Language seleccione entre cientos de algoritmos subyacentes y realice selecciones automatizadas para grandes cantidades de parámetros de algoritmos.
ES TAN FÁCIL QUE SOLO BASTA INTENTARLO
Al reducir drásticamente el costo de probar ideas algorítmicas, Wolfram Algorithmbase ha permitido innumerables descubrimientos e invenciones.
La anatomía de un algoritmo moderno
Los mejores algoritmos en la actualidad habitualmente usan bloques de construcción de áreas muy diferentes, validando la importancia crítica de la integración amplia de Wolfram Algorithmbase.
ESPERE ENCONTRAR SORPRESAS
Incluso cuando un algoritmo en Wolfram Algorithmbase obtiene una respuesta numérica, existe la probabilidad que esté usando computación simbólica por dentro, y tal vez teoría de grafos o geometría computacional.
UNA NUEVA ERA DE ALGORITMOS
Los algoritmos tradicionales a menudo se describen en pseudocódigo de nivel bajo. Actualmente, los mejores algoritmos suelen usar sofisticados bloques de construcción.
NO ES SUFICIENTE OPTIMIZAR EN UN SOLO DOMINIO
Para obtener los mejores resultados para un cálculo numérico, es casi inevitable necesitar capacidades y métodos avanzados fuera del cálculo numérico.
Algoritmos de grado industrial por doquier
El objetivo de Wolfram Algorithmbase no es solo poseer una gran cantidad de algoritmos, sino asegurar que sean precisos, confiables, robustos y completamente escalables en todas las áreas.
UNA TRADICIÓN DE TRES DÉCADAS EN CALIDAD DE SOFTWARE
Wolfram ha sido líder en garantía de calidad de software durante tres décadas, desarrollando extensas metodologías y técnicas algorítmicas para pruebas de software.
LOS USUARIOS MÁS EXIGENTES DEL MUNDO
Los algoritmos Wolfram son usados ampliamente por algunos de los usuarios más exigentes del mundo en áreas como la investigación, desarrollo y el ámbito académico durante tres décadas.
LA MÁS ALTA CALIDAD EN ALGORITMOS
A lo largo de tres décadas, los algoritmos de Wolfram se han vuelto estándares de excelencia en cobertura, precisión y rendimiento en cada vez más dominios.
Más información sobre este producto, comunicarse con:
Luís Franco
Ejecutivo Software Diverso
lfranco@multion.com
+52 (55) 55594050 Ext.118