Promedio bayesiano de modelos (BMA) en el nuevo Stata 18
En el foco de atención: Promedio bayesiano de modelos: ¿No está seguro de cuál es el mejor modelo? ¿Por qué elegir sólo uno? Descubra cómo el promediado bayesiano de modelos y el nuevo comando bmaregress pueden ayudarle en caso de incertidumbre sobre el modelo.
Utilicemos el promedio bayesiano de modelos (Bayesian model averaging, BMA) para investigar cómo influyen los indicadores de salud mental en el tiempo dedicado a los videojuegos utilizando un extracto de este conjunto de datos de Kaggle publicado por Aditi Awasthi.
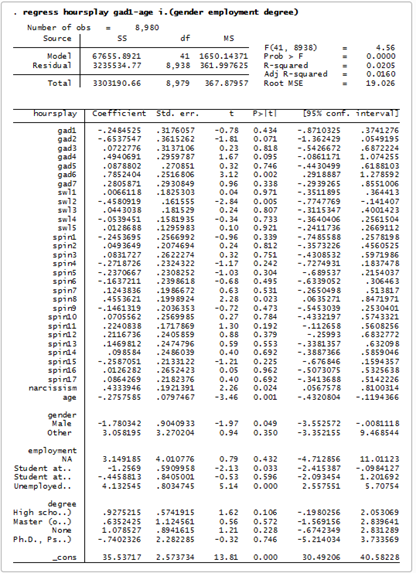
Normalmente, elegimos un modelo y estimamos los parámetros y otras cantidades de interés a partir de los datos observados condicionados a este modelo elegido. Para nuestro ejemplo, nos gustaría ajustar una regresión lineal de las horas dedicadas a los videojuegos en 42 predictores, incluidos los elementos del Inventario de Trastorno de Ansiedad Generalizada (TAG), la Escala de Satisfacción con la Vida (SWL), el Inventario de Fobia Social (SPIN), una medida de narcisismo, la edad, el sexo, la situación laboral y el grado de educación más alto obtenido.
¿Necesitamos los 42 predictores? Probablemente no, pero no sabemos exactamente cuáles incluir. En otras palabras, ¿qué modelo debemos seleccionar? En el caso de la regresión lineal, se pueden utilizar métodos como la regresión por pasos, las pruebas de Wald o incluso los factores de Bayes para seleccionar uno entre los modelos candidatos, pero ¿por qué tenemos que elegir?
Con BMA, tenemos en cuenta la incertidumbre del modelo en nuestro análisis promediando los resultados de todos los modelos plausibles basados en los datos observados. Para ello, consideramos un conjunto de modelos candidatos y estimamos la probabilidad posterior de cada modelo según el Teorema de Bayes. En el contexto de la regresión lineal con p predictores, hay 2p modelos candidatos. A continuación, estimamos los parámetros promediando las estimaciones de los parámetros entre los modelos con pesos de acuerdo con sus probabilidades a posteriori.
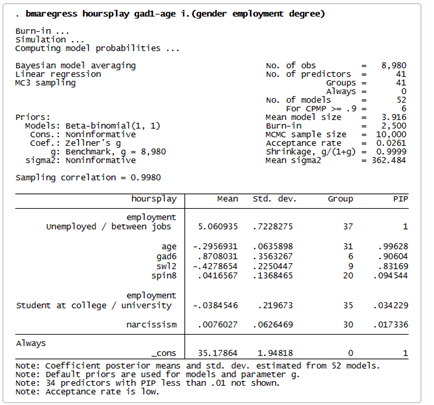
Podemos realizar este análisis utilizando el nuevo comando bmaregress de Stata 18. Al igual que con otros comandos de estimación, enumeramos nuestra variable dependiente seguida de nuestra lista de variables independientes.
La parte superior del resultado nos indica que se exploraron 52 modelos, de los cuales los 6 primeros representan más del 90% de la probabilidad acumulada posterior del modelo. El tamaño medio del modelo fue de 3,9, lo que significa que cada modelo incluía una media de 4 predictores.
La tabla de estimación incluye estimaciones de las medias posteriores y las desviaciones estándar de los coeficientes de cada predictor. De los modelos analizados se deduce que, por término medio, los participantes desempleados pasan 5,06 horas más jugando a videojuegos que los demás grupos de empleo.
También vemos las probabilidades de inclusión posteriores estimadas (PIP). El indicador de desempleo tiene una PIP de 1, lo que significa que se incluyó en todos los modelos explorados. El resto de los predictores se enumeran por orden de sus PIP.
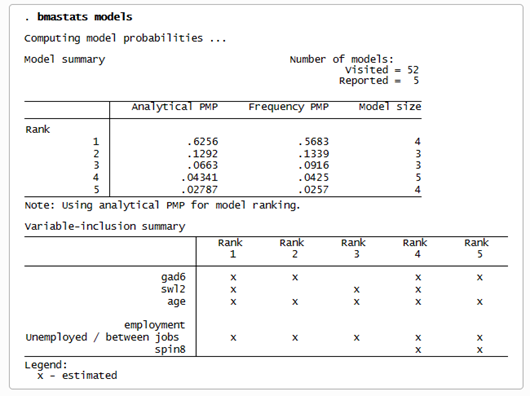
Podemos obtener más información sobre nuestros cinco modelos principales utilizando el comando de postestimación bmastats models.
Ver nota completa:
https://www.stata.com/stata-news/news38-4/bayesian-modeling-averaging/
Más información sobre este producto, entre en contacto con:
Luís Franco
Ejecutivo Software Diverso
lfranco@multion.com
+52 (55) 55594050 Ext.118